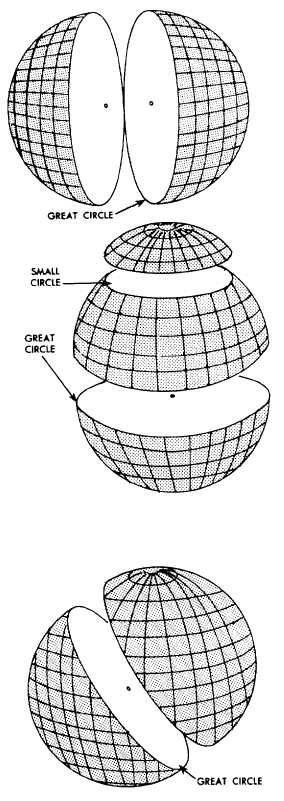
sphere itself. It is the largest circle that can be drawn
on the sphere; it is the intersection with the surface of
the earth of any plane passing through the earth’s
center.
The arc of a great circle is the shortest
distance between two points on a sphere, just as a
straight line is the shortest distance between two
points on a plane.
On any sphere, an infinite
number of great circles may be drawn through
any point, though only one great circle may be
drawn through any two points that are not
diametrically opposite (fig. 2-2).
Circles on the surface of the sphere other than
great circles may be defined as small circles. A small
circle is a circle on the surface of the earth whose
center and/or radius are not that of the sphere. A
special set of small circles, called latitude is discussed
later.
The intersection of a sphere and a plane is a
circle—a great circle if the plane passes through
the center of the sphere, and a small circle if it
does not.
Latitude and Longitude
The nature of a sphere is such that any point on
it is exactly like any other point. There is neither
beginning nor ending as far as differentiation of
points is concerned. So that points may be located
on the earth, some points or lines of reference are
necessary so that other points may be located in
regard to them. The location of New York City with
reference to Washington, D. C., is stated as a number
of miles in a certain direction from Washington,
D.C. Any point on the earth can be located the
same way.
This system does not work well in navigation.
A point could not be precisely located in
m i d - P a c i f i c O c e a n w i t h o u t a n y n e a r by
geographic features to use as a reference. A
system of imaginary reference lines is used to
locate any point on earth. These reference lines
are the parallels of latitude and the meridians of
longitude.
Figure 2-2.-A great circle is the largest circle in a sphere.
LATITUDE.— Each day the earth rotates once on
its north-south axis. This axis terminates at the two
poles. The equator is constructed at the midpoint of
2-3