P = F , or P = 20,000 lb = 2,000 psi
You might compare this to the way you manipulate
10 in.2
A
Ohm's law to find voltage, current, and resistance.
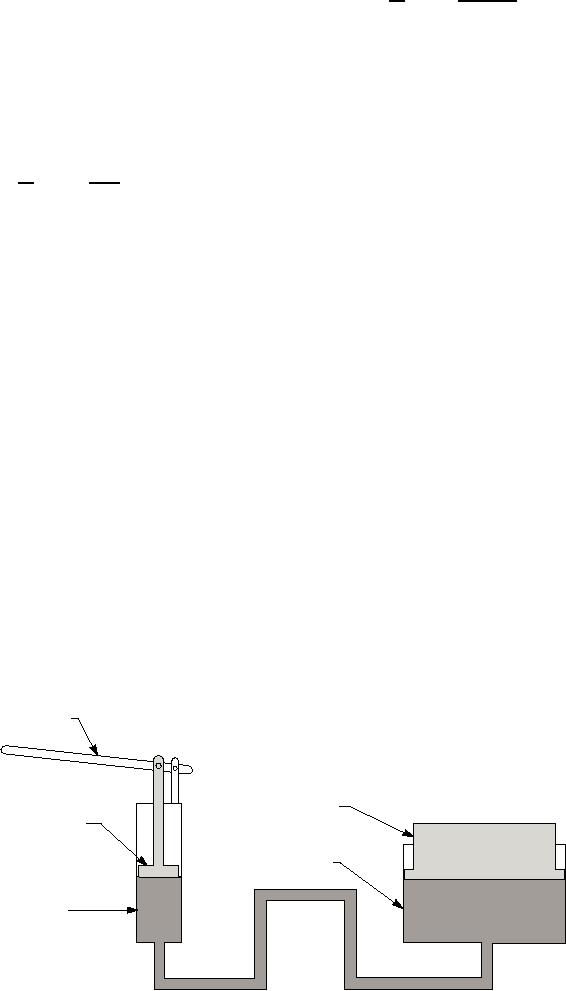
Now, we use this formula to confirm the size of the
To generate the 2,000 psi needed to balance the
pressure developed by piston 1 in the system shown in
10-ton load, a force of 500 pounds must be applied to
figure 8-3.
the top of piston 1.
To find pressure, insert the known values of force
2
(20 lb) and area (2 in.2) into the formula F = PA.
= 500 lb
F = PA, or F = 2,000 psi 0.25 in.
2
Transposing the formula, we have:
The 500 pounds of force applied to piston 1 will
equal the resistant pressure of 2,000 psi and support or
P = F , or P = 20 lb = 10 psi
2 in.2
A
balance the load. To lift the load, however, requires
s o m e t h i n g i n ex c e s s o f 5 0 0 p o u n d s o f f o r c e .
This pressure is applied to the confined liquid
Application of the force can be mechanical, such as by
and, in turn, to all sides of the container, including
the lever shown in figure 8-4, or by motor, or by any
the 20-square-inch area of piston 2. Note that the
other means that will generate the force required by the
upward force exerted by the liquid on piston 2 (F =
10 psi 20 in.2 = 200 lb) is the same as the downward
system. For complete and detailed descriptions of the
2
force (200 lb) exerted by the piston. Thus, the
c l a s s e s o f l eve r s , c o n s u l t B a s i c M a ch i n e s ,
20-pound force applied to piston 1 supports a force
NAVEDTRA 14037.
of 200 pounds acting against piston 2.
Q8-1. Which of the following is NOT a
You should remember that the force exerted on
characteristic of a liquid?
piston 1 (20 lb) only creates a flow of liquid. and that
1.
A liquid can only be slightly compressed
the resistance force (200 lb) is required to create
2.
A liquid has no definite shape
pressure. With no resistance against piston 2, any force
3.
A liquid has the ability to transmit power
exerted on piston 1 will develop only that pressure
4.
A liquid can be compressed to half of its
resulting from the friction of liquid flow and the weight
original volume
of piston 2.
Q8-2. Which of the following laws state that,
For a more realistic application of multiplication
"pressure applied to an enclosed or confined
of forces, consider the 10-ton hydraulic jack system
fluid is transmitted equally in all directions
shown in figure 8-4. Assume that piston 2 is the
without loss and acts with equal force on
lifting piston, with an area of 10 square inches, and
equal surfaces"?
that piston 1 is the pump, with an area of 0.25 square
inch. Next, assume that a 10-ton (20,000 pounds)
1.
Boyle's law
load is placed on piston 2. To support this force, a
2.
Pascal's law
pressure of 2,000 psi must be exerted against the
3.
Stanton's law
4.
Ohm's law
bottom of piston 2.
HANDLE
PUMP
10-TON LOAD
500 LB
PISTON 2
(20,000 LB)
PISTON 1
10 SQ. IN.
0.25 SQ. IN.
CYLINDER 2
CYLINDER 1
ASf08004
Figure 8-4.--A 10-ton hydraulic jack.
8-4



