realigns the suspending string with the new local
The formula shows that the period of a
gravity vector. Therefore, the angular motion of
simple pendulum is proportional to the square
the pendulum about the gravity vector for any
root of the length of the suspending string. The
horizontal acceleration of the suspension point is
longer the string, the longer the period.
zero. This particular pendulum is the Schuler
One property of the simple pendulum that is
very useful in the construction of an inertial
pendulum, shown in figure 7-40, view B. This
pendulum gets its name from the German
stable element is shown in figure 7-41. Two
engineer, Maximilian Schuler.
pendulums are suspended by strings of different
Schuler solved the problem of oscillating
lengths. Equal forces horizontally accelerate the
shipboard gyrocompasses in the early 1900s. Of
suspension point of each pendulum. The inertia
course, Schuler couldn't use the simple pendulum
of the bob resists the change in its state of
itself to solve this oscillating problem. He used
motion. This action causes the bob to lag the point
of suspension. It also produces an angular
the principle of the simple pendulum to construct
a pendulum that reacted like a simple pendulum.
motion of the pendulum about the local gravity
The length of this pendulum equals the radius of
vector. Figure 7-41 shows that the length of
the earth, which is about 3,440 nautical miles long.
pendulum (B) is longer than pendulum (A). It also
The period of oscillation for this pendulum is
shows angular motion of pendulum (B) is less than
about 84.4 minutes. Remember the period of
pendulum (A) for a corresponding linear motion
oscillation of a pendulum is proportional to the
of the suspension point. Therefore, the longer the
square root of its length. Therefore, any pen-
suspending string, the less the angular motion of
dulum constructed to oscillate with a period of
the pendulum for a given linear motion of the
84.4 minutes would have an equivalent length of
suspension point.
Consider what would happen in the following
about 3,440 nautical miles. Such a pendulum is
the Schuler pendulum, a special case of the
case. The suspending string is long enough to
compound or physical pendulum. Figure 7-42
maintain the bob at the center of the earth. The
shows three examples of compound pendulums.
suspension point is transported horizontally along
the earth's surface (fig. 7-40, view B). The bob
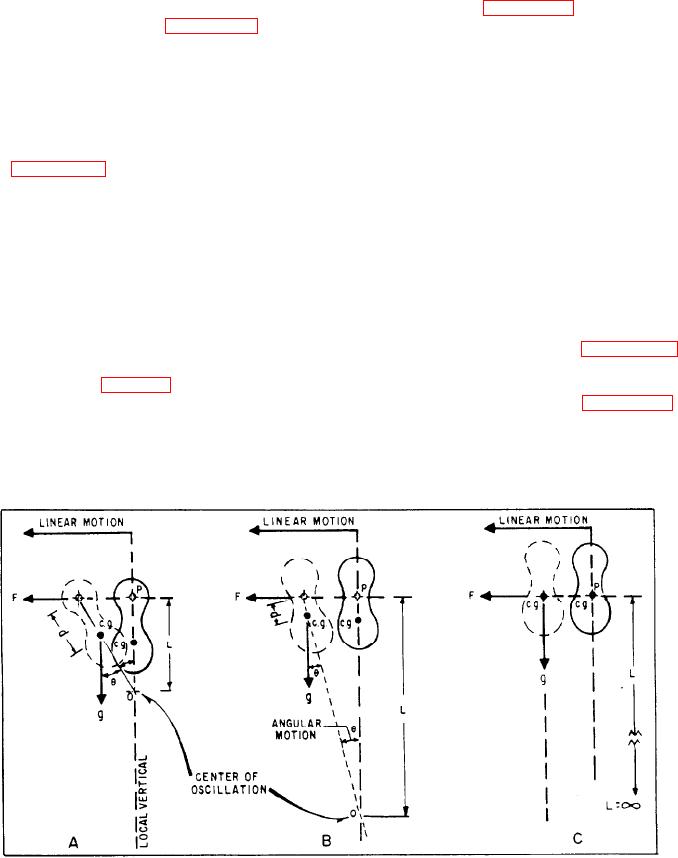
COMPOUND PENDULUM. --In figure 7-42,
is hypothetically at the center of the earth, the seat
view A, the pivot point, P, is farthest away from
of the earth's gravity field. Accelerating the
the center of gravity, represented by distance d.
suspension point along the earth's surface merely
Figure 7-42.-Compound pendulum.
7-33

